Discrete
Distribution
Family

Binomial distribution family

Yu Cheng Hsu

Intended learning outcomes

  • Recognize and apply Bernoulli and binomial distributions in statistical models
  • Derive the binomial and negative binomial distributions

Bernoulli distribution

If a random variable \(X\) follows bernoulli distribution, we will write \(X \sim \text{Bernoulli}(p)\)

Properties

  • Support \(\mathbf{X} = \{0, 1\}\)
  • Parameter \(p \in [0, 1]\) is the probability of success.
  • pmf

\[ \begin{align} P ( X = x \mid p ) \; & = \; p^x \, (1 - p)^{1 - x} \\ & = \begin{cases} p \quad & \text{if } x=1 \\ 1 - p \quad & \text{if } x=0 \end{cases} \end{align} \]

  • Mean: \(\mathbf{E}(X) = p\)
  • Variance: \(\mathbf{V}(X) = p(1-p)\)

Analogy

Tossing a coin for one time. The head or tail follows bernoulli distribution

Bernoulli trials

Suppose we have \(N\) iid trials with success probability \(p\), resulting in random variables \(\mathbf{X} = [X_1, \ldots, X_N]\) such that \[ X_i \sim \text{Bernoulli}(p) . \] This sequence of iid trials are called Bernoulli trials. \[ \begin{aligned} P_{\mathbf{X}}\left( \mathbf{x} \right) &= \prod_{i=1}^N P_{X_i}\left(x_i\right) \quad (\text{independent}) \\ &= \prod_{i=1}^N p^{x_i} (1- p)^{1 - x_i} \\ &= p^{\sum_i x_i} (1- p)^{N - \sum_i x_i} \end{aligned} \]

Examples

Suppose we are tossing 5 unfair coins with the \(p(\text{head}) = 0.3\) and \(p(\text{tail}) = 0.7\). What is the probability of getting observation [T, T ,T, H, H]

\(p(X=[T, T ,T, H, H])=0.7^3\times 0.7^2\)=0.03087

Bernoulli trials

We define a new r.v. \(\small Y = \sum_{i=1}^N X_i\). Then, for \(\small y \in \{0, 1, \ldots, N\}\), (i.e. Y is the number of head from a fixed length bernoulli trials)

\[ \small \begin{aligned} P_Y \left( y \right) = P \left( \left\{ \mathbf{x} : \sum_i x_i = y \right\} \right) = \binom{N}{y} P_{\mathbf{X}}\left( \mathbf{x} \right) = \binom{N}{y} p^y \, (1 - p)^{N - y} . \end{aligned} \]

Recall from previously, then we have derived the binomial distribution.

\(y\) Outcome Probability # permutation
0 \(\{ 000 \}\) \((1-p)^3\) \(\binom{3}{0}\)
1 \(\{ 100, 010, 001 \}\) \(p(1-p)^2\) \(\binom{3}{1}\)
2 \(\{ 110, 101, 011 \}\) \(p^2(1-p)\) \(\binom{3}{2}\)
3 \(\{ 111 \}\) \(p^3\) \(\binom{3}{3}\)

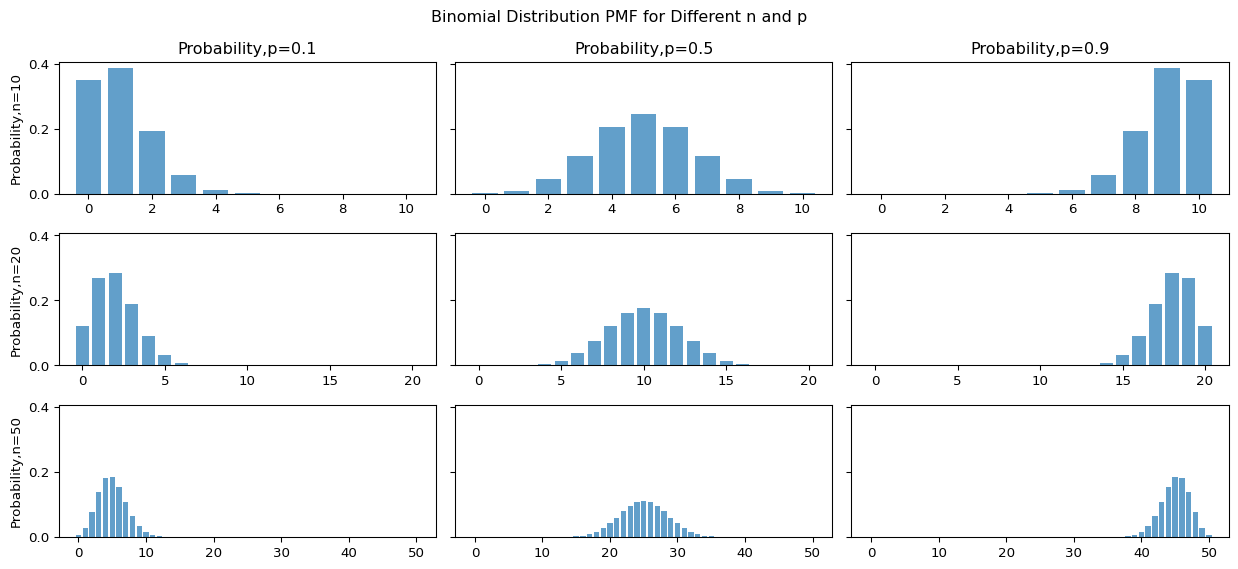
Binomial distribution

If a random variable \(X\) has a binomial distribution, we will write \(X \sim B(N,p)\).

Properties

  • Support \(\mathcal{X} \in \{0, 1, \ldots, N\}\)
  • Parameter \(N, p\), where
    • \(p \in [0, 1]\) is the probability of success
    • \(N\) is number of trials.
  • pmf

\[ \small \begin{aligned} & P\left( X = x \mid N, p \right) = \binom{N}{x} p^x \, (1 - p)^{N - x} \end{aligned} \]

  • Expectation: \(\mathbb{E}(X) = Np\)
  • Variance: \(\mathbb{V}(X) = Np(1-p)\)

Analogy

We are tossing an unfair coins for 10 times with \(p(H) = 0.3\). What is the probability of

  1. getting 3 heads and 7 tails
  2. getting 7 heads and 3 tails

Illustration

import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import binom

def plot_binomial_pmf(ns, ps):
    """
    Plot the PMF of binomial distributions for different n and p values.
    
    Parameters:
    - ns: list of integers, different number of trials (N)
    - ps: list of floats, different success probabilities (p)
    """
    fig, axs = plt.subplots(len(ns), len(ps), figsize=(13, 6), sharey=True)
    fig.suptitle('Binomial Distribution PMF for Different n and p')
    
    for i, n in enumerate(ns):
        for j, p in enumerate(ps):
            # Possible k values
            k = np.arange(0, n+1)
            # PMF values
            pmf = binom.pmf(k, n, p)
            
            # Plot as bar chart
            axs[i, j].bar(k, pmf, alpha=0.7)
            if j == 0:
                axs[i, j].set_ylabel(f'Probability,n={n}')
            if i == 0:
                axs[i, j].set_title(f'Probability,p={p}')
    
    plt.tight_layout()
    plt.show()

# Example usage
if __name__ == "__main__":
    ns = [10, 20, 50]  # Different N values
    ps = [0.1, 0.5, 0.9]  # Different p values
    plot_binomial_pmf(ns, ps)

Example: Wright-Fisher Model (Optional)

Consider a populaton with \(N\) diploid individuals. and we are interested in an allele with possibile genotypes \(A\) and \(a\)

  • Each individual in the population produces a large number of gametes.
  • Fixed population size
  • Mendelian inheritance applied

Please describing the probability that there will be \(n_{A1}\) copies of \(A\) in the next generation given that there are \(n_{A0}\) copies in the parent generation:

\[ p(n_{A1} \text{in offspring}\mid n_{A0} \text{in parents})=\binom{2N}{n_{A1}}( \frac{n_{A0}}{2N} )^{n_{A1}}( 1-\frac{n_{A0}}{2N} )^{2N-n_{A1}} \]

Some Properties on Binomial distribution

  1. it is obvious us that p(x) for a binomial distribution is the (x+1)-th term in the expansion of \([p + (1-p)]^N\) (Binomial theorm)
  2. In this end, it is clear that binomial distribution satisfy the axiom

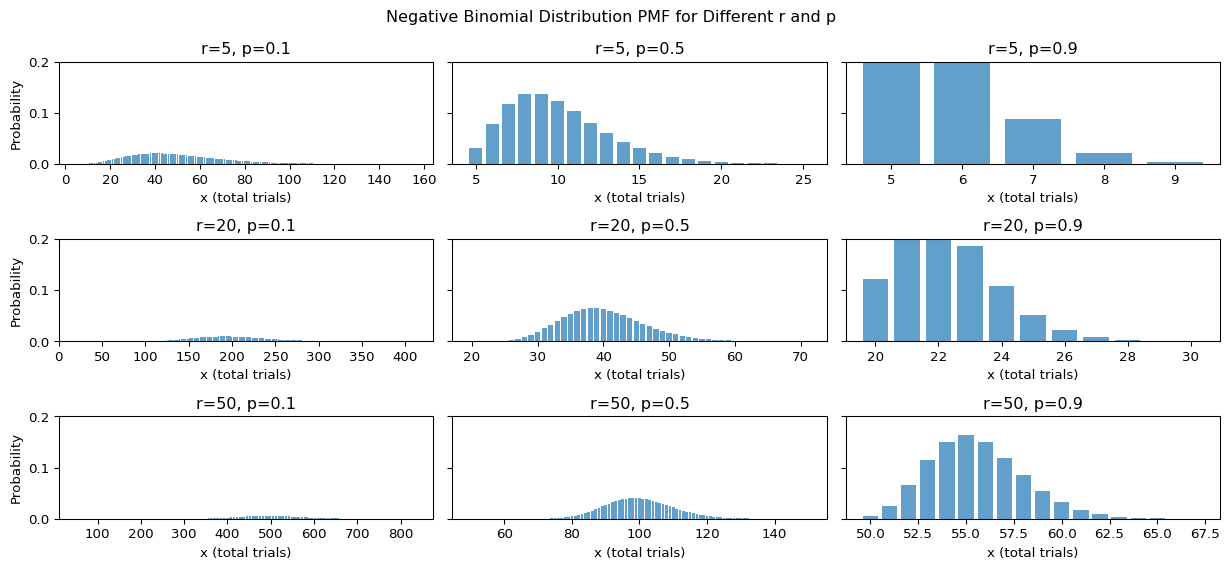
Negative binomial distribution

We define the random variable \(X\) as how many time we need to toss until the r-th success. \(X\) follows negative binomial distribution (\(X\sim NB(r,p)\))

Properties

  • Support \(x\in\{ \mathbb{N} \mid\quad\forall \mathbb{N}>r\}\)
  • Parameter \(r,p\)
  • pmf

\[ P\left( X = x \mid r, p \right) \; = \; \binom{x - 1}{r - 1} p^r (1 - p)^{x - r} \]

  • Mean \(\frac{r(1-p)}{p}\)
  • Variance \(\frac{r(1-p)}{p^2}\)

Analogy

  • Tossing coins to see how many times it take to see the 5-th head
  • Gene expression

Illustration

import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import nbinom

def plot_negative_binomial_pmf(rs, ps, max_multiplier=5):
    """
    Plot the PMF of negative binomial distributions for different r (number of successes) and p values.
    Here, X = k + r, where k is the number of failures before r successes, and X is the total number of trials.
    
    Parameters:
    - rs: list of integers, different number of successes (r, often denoted as n in some contexts)
    - ps: list of floats, different success probabilities (p)
    - max_multiplier: int, multiplier for max_k to truncate the plot (default 5)
    """
    fig, axs = plt.subplots(len(rs), len(ps), figsize=(13, 6), sharey=True)
    fig.suptitle('Negative Binomial Distribution PMF for Different r and p')
    
    for i, r in enumerate(rs):
        for j, p in enumerate(ps):
            # Mean and variance for truncation
            mean_failures = r * (1 - p) / p
            var_failures = r * (1 - p) / p**2
            max_k = int(mean_failures + max_multiplier * np.sqrt(var_failures))
            
            # k values (failures)
            k = np.arange(0, max_k + 1)
            # x values (total trials)
            x = k + r
            # PMF values for X (same as for k)
            pmf = nbinom.pmf(k, r, p)
            
            # Plot as bar chart
            axs[i, j].bar(x, pmf, alpha=0.7)
            axs[i, j].set_title(f'r={r}, p={p}')
            axs[i, j].set_xlabel('x (total trials)')
            if j == 0:
                axs[i, j].set_ylabel('Probability')
            elif j ==1:
                axs[i, j].set_ylim(0,0.3)
            elif j ==2:
                axs[i, j].set_ylim(0,0.2)
    plt.tight_layout()
    plt.show()

# Example usage
if __name__ == "__main__":
    rs = [5, 20, 50]  # Different r values (number of successes)
    ps = [0.1, 0.5, 0.9]  # Different p values
    plot_negative_binomial_pmf(rs, ps)

Geometric distribution

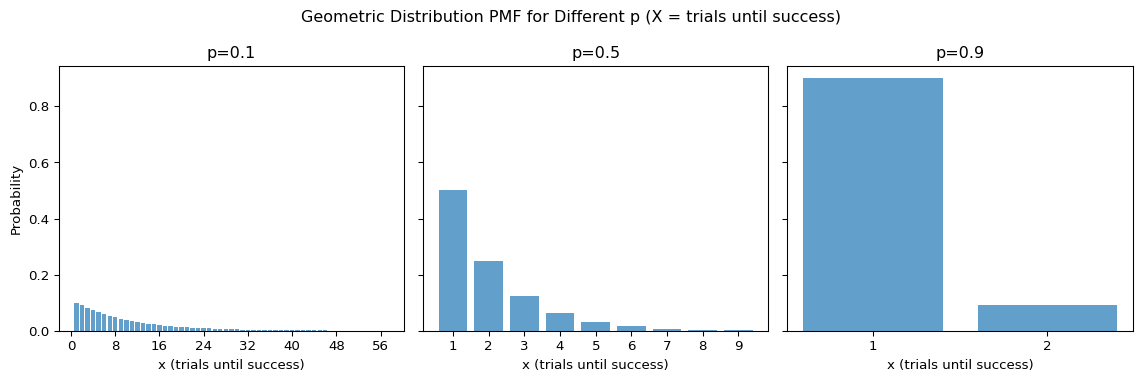
A geometric distribution special case of the negative binomial distribution where \(r = 1\).

A random variable \(X \sim G(p)\) follows geometric distribution has the following property

Properties

  • Support \(x \in \mathbb{N}\)
  • Parameter \(p\) is the probability of success
  • pmf

\[ P\left( X = x \mid p \right) \; = \; p (1 - p)^{x - 1} \]

  • Mean \(\frac{1}{p}\)
  • Variance \(\frac{(1-p)}{p^2}\)

Analogy

A mobile game has a 5% draw a SSR card. In average, how many draws do you need to get a SSR card?

Illustration

import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import geom
import matplotlib.ticker as ticker
def plot_geometric_pmf(ps, max_multiplier=5):
    """
    Plot the PMF of geometric distributions for different p values.
    Here, X is the number of trials until the first success.
    
    Parameters:
    - ps: list of floats, different success probabilities (p)
    - max_multiplier: int, multiplier for max_x to truncate the plot (default 5)
    """
    fig, axs = plt.subplots(1, len(ps), figsize=(12, 4), sharey=True)
    fig.suptitle('Geometric Distribution PMF for Different p (X = trials until success)')
    
    for j, p in enumerate(ps):
        # Mean and variance for truncation
        mean = 1 / p
        var = (1 - p) / p**2
        max_x = int(mean + max_multiplier * np.sqrt(var))
        
        # x values (trials)
        x = np.arange(1, max_x + 1)
        # PMF values
        pmf = geom.pmf(x, p)
        
        # Plot as bar chart
        axs[j].bar(x, pmf, alpha=0.7)
        axs[j].set_title(f'p={p}')
        axs[j].set_xlabel('x (trials until success)')
        if j == 0:
            axs[j].set_ylabel('Probability')

        # Adjust xticks to only show at integers
        axs[j].xaxis.set_major_locator(ticker.MaxNLocator(integer=True))

    plt.tight_layout()
    plt.show()

# Example usage
if __name__ == "__main__":
    ps = [0.1, 0.5, 0.9]  # Different p values
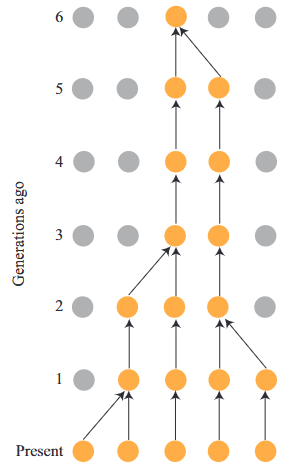
    plot_geometric_pmf(ps)

Example: Coalescent (Optional)

The probability that two alleles in generation \(t\) are copies of the same allele in generation \(t − 1\) is \(\frac{1}{2N_e}\) (i.e. probaility to coalesce).

For a coalescent event occur at \(t\) generation ago, it means that two alleles have NOT have colleased in the \(1 \dots t-1\) generation ago.

The probability that two alleles coalesced t generations ago

\[ P(T=t)=(1-\frac{1}{2N_e})^{t-1}(\frac{1}{2N_e}) \]

Coalescent illustration from @nakagome2015use

Coalescent illustration from @nakagome2015use

Hypergeometric distribution

Tthis time we draws sample without replacement from the finite sample \(N\) with known \(K\) succeess and the random variable \(X\) is defined as exactly \(x\) times of success with \(n\) draws. \(X\sim\text{Hypergeometric}(N,K,n)\)

Properties

  • Support \(x \in {\max(0,n+K-N),\dots,\min(n,K)}\)
  • Parameter \(N, K, n\)
  • pmf

\(P( X = x) = \frac{\binom{K}{x}\binom{N-K}{n-x}}{\binom{N}{n}}\)

  • Mean \(n\frac{K}{N}\)
  • Variance \(n\frac{K}{N}\frac{N-K}{N}\frac{N-n}{N-1}\)

Analogy

Choosing 5 red balls and 3 blue balls from total 10 red balls and 15 blue balls without replacement

Example: Fisher’s exact test

We can view the p-value in Fisher’s exact test as the cdf of a hypergeometric disstribution.

Tretment Control Row sum
Y a b M
Not Y c d N-M
Column sum n N-n N

Fisher’s exact value assumes

the row sum&column sum value fixed

Observation of contingency table follows hypergeometric distribution with the probability:

\[ p(x=a) = \frac{\binom{M}{a}\binom{N-M}{n-a}}{\binom{N}{n}} \]

Example: Capture and Re-capture Experiment (Optional)

To estimate the population size of a specific animal in a certain region, the ecologists erform the following procedure (This methods were adopted in counting counting health survey, microbome)

  1. Catch \(m\) animal from the site, label them with marker and release.
  2. After a couple of time, catch \(n\) animal from the lake.

We denoted the number of marked animal as \(X\) and it is obvious that \(X\) follow hypergeometric distribution

In our experiment

  • \(n\) animal caught
  • \(i\) marked animal

so the probability of having \(i\) given the the unknown population parameter \(N\) is

\[ P(X=i | N)\frac{\binom{M}{i}\binom{N-M}{n-i}}{\binom{N}{n}} \]

Example: Capture and Re-capture Experiment (Optional)

  • Finding optimal \(N\) is tough
  • Trick: Consider

\[r=\frac{P(X=i | N)}{P(X=i | N-1)}\]

  • \(P(X=i | N)\geq P(X=i | N-1)\) (i.e. \(r\geq 1\)) then we should use the parameter N as the estimation rather than \(N-1\)
  • Optimal N will at the boundary condition

The boundary condition will be

\[ \begin{aligned} (N-m)(N-n) \geq & N(N-m-n+i) \\ \rightarrow & N \leq \frac{mn}{i} \end{aligned} \]

The best estimation of population size the larget integer less than \(\frac{mn}{i}\)